图论专题学习笔记

注意：正如题目所言，本篇文章是学习笔记，只记录了某个知识点的框架和重点，具体内容请参照其它文章

第一部分：最小生成树

性质：

• 边权和最小
• 任意两点之间的最大边权最小

Kruskal 重构树

Kruskal

• 将边从小到大排序
• 按顺序一条一条试（贪心思想，不需要反悔）

简单应用

多次询问，每次从 $u$ 出发，经过不超过 $w$ 的边能到哪些点

直接套 Kruskal，然后求连通块大小就行了

建树

仿照 Kruskal 的过程，把每个点用并查集连起来换成在树上将其连起来，即把每一个操作作为树的一个节点，像这样：

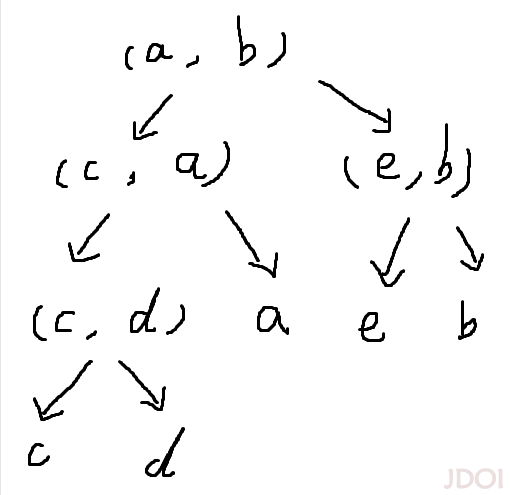
随便画的，将就看看吧

性质

• 将边权和转化为了点权和

• 祖先节点的权值一定大于后代（因为祖先节点后加入）

• 从 $u$ 到 $v$ 的边权的最大权值的最小值为 $LCA(u,v)$

• 对于上面的题，我们只需要找到 $u$ 的祖先中，最后被加入的小于等于 $w$ 的边，那么它的子树中的所有点都是能够到达的。这样我们就可以将求连通块的问题转化成研究子树的问题

例题

NOI2018 归程

关于 SPFA，它死了

• 车：经过 $a>p$ 的任意边（能到达重构树的子树）
• 步行：求子树内每个点到 $1$ 的最短路

具体的当然就自己去看题解啦（其实我也不会，码力太弱了）

第二部分：最短路

01-最短路

双端队列 BFS

SPFA

只用来解决带负权边的图，否则死的就是你

容易被卡的原因：在菊花图中会退化到 $O(nm)$

Dijkstra

解决正边权问题，常见优化：

• priority-queue：$O(m\log m)$
• zkw 线段树：$O(m\log n)$
• 斐波那契堆：$O(n\log n)$

边权较小的最短路问题

• 拆边，$n+mw$ 个点，$nw$ 条边，转化为全 $1$ 最短路

• 拆点，$nw$ 个点，$nw+m$ 条边，也是转化为全 $1$ 最短路

差分约束

差分约束 - OI Wiki (oi-wiki.org)

SPFA 活了

2023/4/18 更新

同余最短路

P2371 墨墨的等式

第三部分：连通性相关

前置知识：$tarjan$

2-SAT

有 $n$ 个 $0/1$ 变量 $x_1\sim x_n$ ，$m$ 个形如 “若 $(\neg)x_i$ ，则 $(\neg)x_j$ ”的命题，判断/构造一组合法的 $x_1\sim x_n$

• 建立 $2n$ 个点：$x_1\sim x_n$，$\neg x_1 \sim \neg x_n$
• 对于每一个命题及其逆否命题，从 $(\neg)x_i$ 到 $(\neg)x_j$ 连一条有向边
• 这样一来，图上的到达关系等价于推出关系，即图上的某点能到达另一点，那它一定能推出那个点
• 如果发现 $x_i$ 能到达 $\neg x_i$ ，就说明 $x_i=0$
• 同样的，如果 $\neg x_i$ 能到达 $x_i$ ，则说明 $x_i=1$
• 当以上两种情况同时出现，即 $x_i$ 与 $\neg x_i$ 在同一个 SCC（强连通分量）里，则不存在合法情况

接下来是利用 $tarjan$ 的性质构造一组合法情况

• 我们知道 $tarjan$ 是给每个 SCC 编号，且这个编号满足拓扑序倒序，用 $bel_j$ 表示 $i$ 所在的 SCC
• 如果 $bel_i>bel_j$ ，那么 $j$ 一定无法到达 $i$
• 我们对于每个 $x_i$ ，判断 $bel_{x_i}$ 和 $bel_{\neg x_i}$ 的大小关系，如果前者大，$x_i=0$ ；反之，$x_i=1$
• 证明略（我不会），但可以证明是充分且必要的

P4782 【模板】2-SAT 问题
#3629. 「2021 集训队互测」序列

圆方树

• 点双与点双之间通过割点连接
• 将点双建成一个虚点（方点），割点建成实点（圆点）

这个图有一下性质：

• 圆点只连方点，方点只连圆点
• 这个图是一个树

这棵树就叫圆方树

建树

P3388 【模板】割点（割顶）

性质

• 叶子节点一定是圆点
• 圆点中非叶节点即为割点
• 原来的图上 $u$ 到 $v$ 的必经点就是圆方树上 $u$ 到 $v$ 上的所有圆点

P4606 战略游戏

第四部分：网络流

网络流与线性规划 24 题