[SDOI2010] 地精部落题解

传送门

简要题意：求长为 $n$ 的排列的波动序列的个数。

考虑 DP，设 $f_{i,j}$ 表示长度为 $i$ 的排列中，不合法元素有 $j$ 个的方案数，其中不合法元素指的是一个排列里既不是山峰也不是山谷的元素。显然我们最后要的答案即为 $f_{n,0}$。下面考虑转移

可以考虑如何从 $f_i$ 推 $f_{i+1}$。这其实相当于在长度为 $i$ 的排列中插入一个数 $i+1$，显然 $i+1$ 就是是这个排列里最大的数了。容易发现，插入这个数后这个排列的不合法元素要么不变，要么加一，要么减一，那么我们分别分析这三种情况。

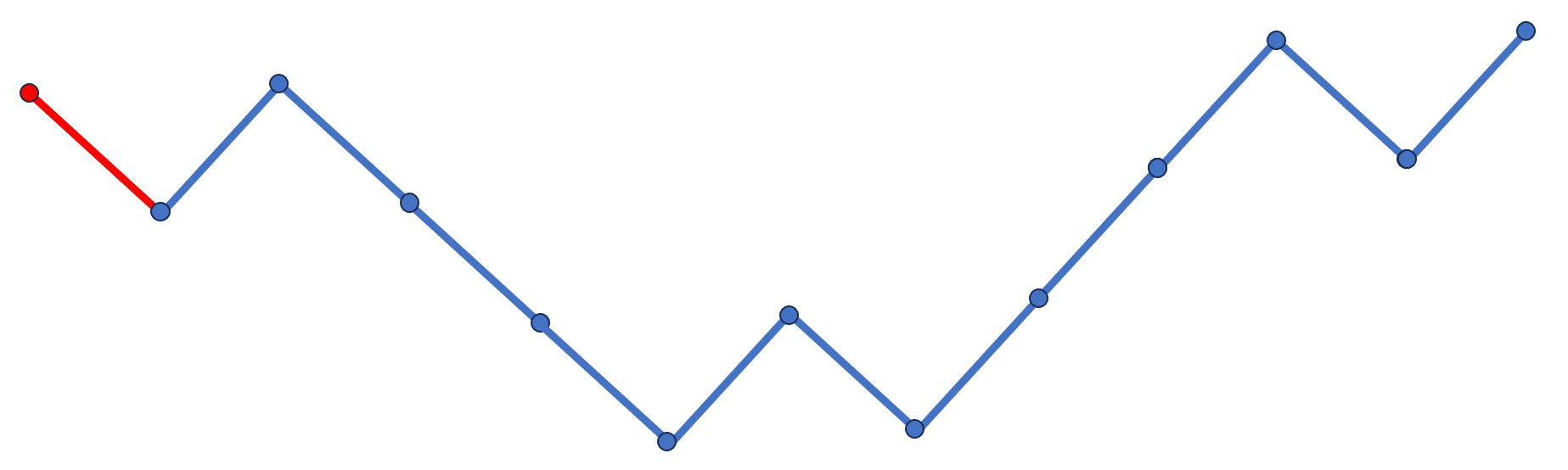
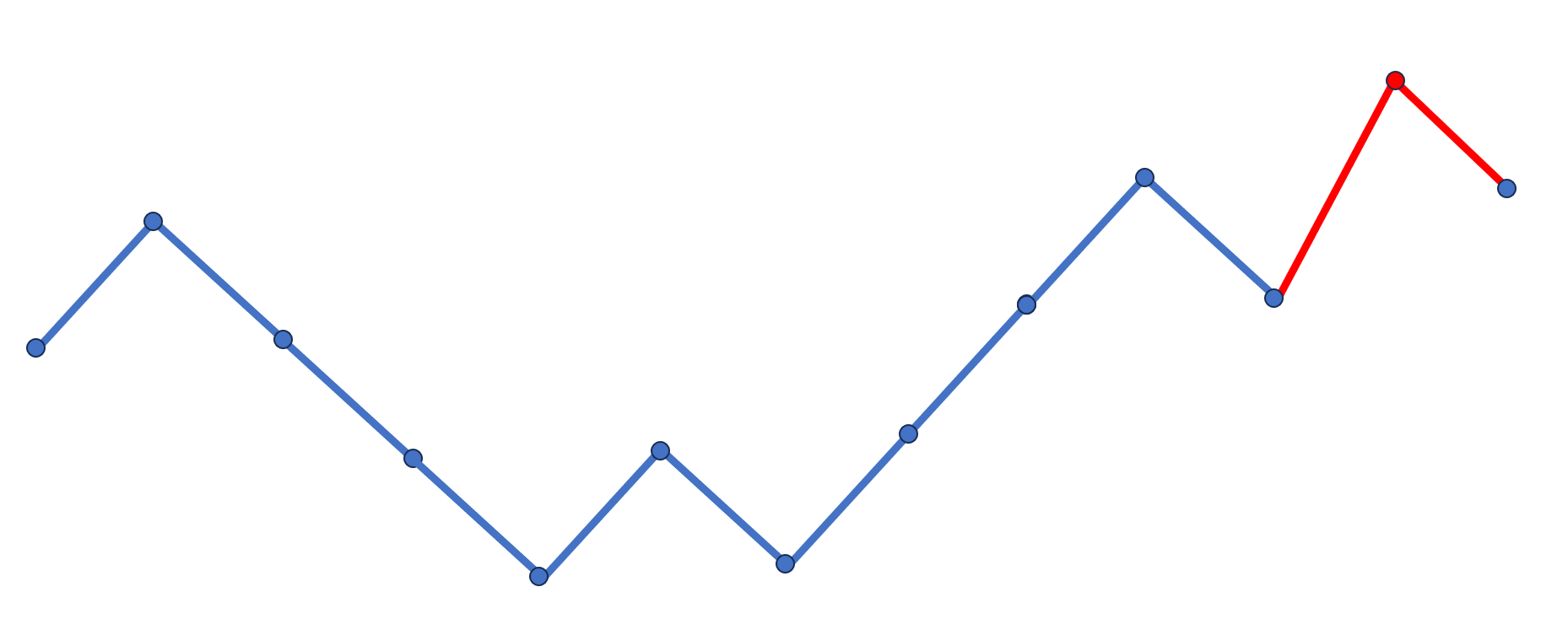
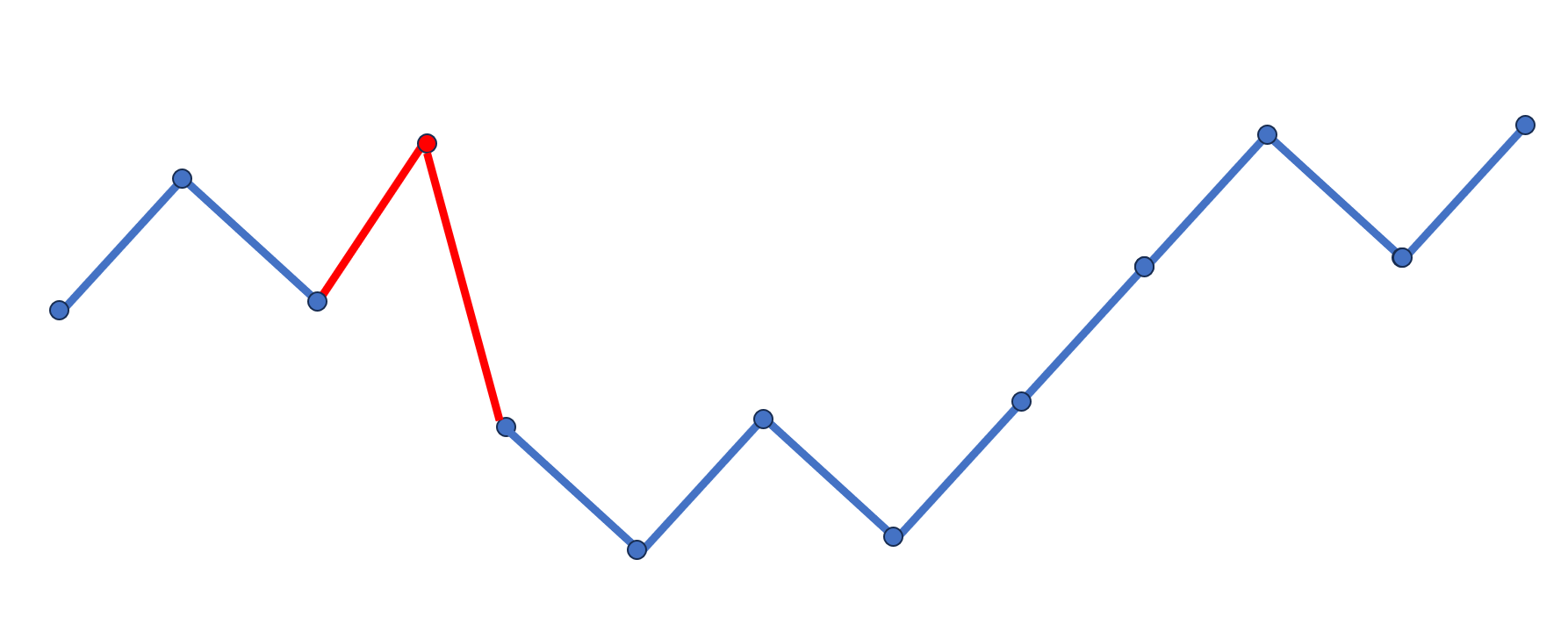
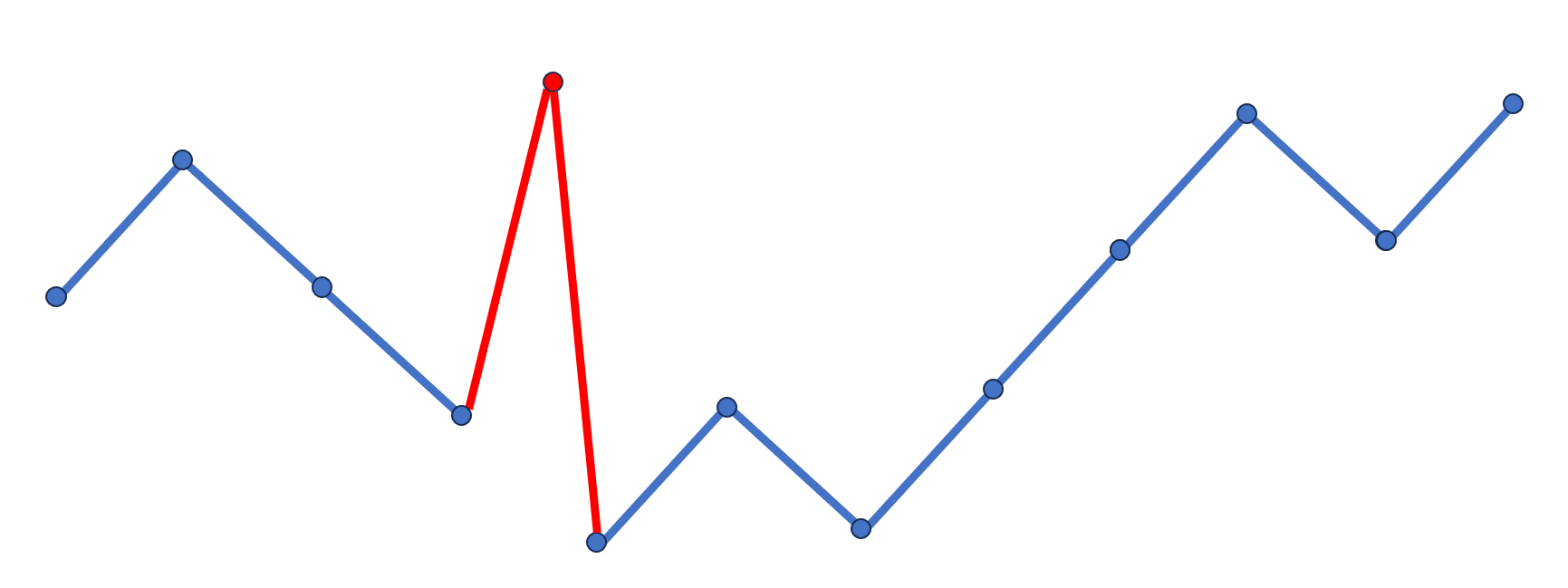
为了方便，先给个示意图（这个图当然很不严谨，但我个人认为比较直观）：

不合法元素数量不变

• 当边界是山谷，把新元素插入到边界之外，即：

• 当边界是山峰，把新元素插在 边界 和 与边界相邻的点 之间，即：

由于两个边界一定是山峰或者山谷，因此我们可获得的新的状态就是原来个数的两倍，即：

$$f_{i+1,j}=f_{i+1,j}+f_{i,j}\times 2$$

不合法元素数量减一

• 对于每个 比它左边的元素小的 不合法元素，把新元素插在其右边，即：

  或：

• 对于每个 比它左边元素大的 不合法元素，把新元素插在其左边，即：

  或：

也就是说，对于每个不合法元素，我们都有一种插入方案使得新排列的不合法元素数量减一，即：

$$f_{i+1,j-1}=f_{i+1,j-1}+f_{i,j}\times j$$

不合法元素数量加一

由于长为 $i$ 的排列有 $i+1$ 个位置是可插入的，而前面已经插入了 $2+j$ 个位置，所以剩下的 $i-j-1$ 个位置都会使不合法元素数量加一，即：

$$f_{i+1,j+1}=f_{i+1,j+1}+f_{i,j}\times (i-j-1)$$

推出了转移方程这道题也就解决了，实现时注意用滚动数组即可。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
typedef long long ll;
const int maxn = 4205;
int n, mod;
int f[2][maxn];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> n >> mod;
    f[1][0] = 4, f[1][1] = 2;
    for (int i = 3; i < n; i++)
    {
        int nxt = ((i + 1) & 1), now = (i & 1);
        for (int j = 0; j <= i - 1; j++)
            f[nxt][j] = 0;
        for (int j = 0; j <= i - 2; j++)
        {
            f[nxt][j] = (f[nxt][j] + 1ll * f[now][j] * 2 % mod) % mod;
            if (j)
                f[nxt][j - 1] = (f[nxt][j - 1] + 1ll * f[now][j] * j % mod) % mod;
            f[nxt][j + 1] = (f[nxt][j + 1] + 1ll * f[now][j] * (i - j - 1) % mod) % mod;
        }
    }
    cout << f[n & 1][0] << endl;
    return 0;
}

这道题的为什么是蓝题？感觉思维难度至少紫啊